平方数とは、ある整数の平方(=二乗)であるような整数のことを言います。つまり、0,1,4,9,16,...が平方数ということになります。
ところで、与えられた整数が平方数かどうかを判定するにはどうすれば良いでしょうか。与えられた整数の平方根の小数点以下を切り捨て、それを二乗して元の数になるかどうか、というのがすぐ思いつく実装です。
<?php function is_square($n) { $sqrt = floor(sqrt($n)); return ($sqrt*$sqrt == $n); }
しかし、平方根の計算は比較的重い処理です。もっと高速化する方法は無いのでしょうか。
多倍長整数演算ライブラリGNU MPには平方数かどうかを判定するmpz_perfect_square_p関数が存在します(PHPでもgmp_perfect_square関数として利用できます)。本稿ではこの実装で使われている工夫を紹介します。
GNU MPのmpz_perfect_square_p関数の実装
GNU MPのソースコードを確認してみたところ、mpz_perfect_square_p関数の実体は低レベル関数であるmpn_perfect_square_pのようです。そこでmpn/generic/perfsqr.cを確認してみると、次のような処理だとわかります。
- 引数nのmod 256を計算し、平方数ではない数を判定する
- 平方数のmod 256は44種類の値しか出現しないので、入力の82.8%は平方数でないと判定できる
- 同様に入力nのmod 9, 5, 7, 13, 17(64-bitシステムではmod 97も)を計算し、平方数ではない数を判定する
- これにより入力の99.25%(64-bitシステムでは99.62%)について平方数でないと判定できる
- 最後に、平方根を計算して平方数かどうか確認する
平方数ではない数の多くを事前にふるい落とし、判定できなかった数だけ真面目に平方根を求める、という方針だとわかります。平方数でない数の判定にmod pを計算するというのは多くの場合に有効な方法です。
もちろん、GNU MPの場合のmod pの選び方は多倍長整数演算ならではだと言えます。多倍長整数は32bitや64bit整数の配列を一つの整数として扱うようなものですから、たいていの演算は多倍長整数のサイズNが大きくなるほど時間がかかります。一方で、mod 256はサイズNにかかわらずO(1)で計算できるので、最初に行うことで全体の高速化に貢献できます。
また、2ステップ目の計算も2^24-1 = 9 * 5 * 7 * 13 * 17 * ...であることを利用し、多倍長整数であっても比較的高速に計算できるような実装になっています。10進整数でmod 9を求める場合に全部の桁を足し合わせてからmod 9しても同じ結果になるのと同様、下位から24bit区切りの数を足し合わせてからmod 2^24-1を計算することで、元の数のmod 2^24-1が計算できるのです。
mod pの世界の平方数
平方根を求めなくてもmod pを計算すれば平方数でない数が判定できるというのは興味深い内容ですよね。しかし、どんなpを選べば平方数でない数を判定できるのでしょうか。平方数が取りえない値は必ず存在するのでしょうか。
小さい奇素数pを選んで、n^2 mod pが取りうる値を調べてみましょう。
| p | n^2 mod pの取りうる値 | その個数 |
|---|---|---|
| 3 | 0,1 | 2 |
| 5 | 0,1,4 | 3 |
| 7 | 0,1,2,4 | 4 |
| 11 | 0,1,3,4,5,9 | 6 |
| 13 | 0,1,3,4,9,10,12 | 7 |
| 17 | 0,1,2,4,8,9,13,15,16 | 9 |
| 19 | 0,1,4,5,6,7,9,11,16,17 | 10 |
面白いことに、全てのpについてn^2 mod pが取りえない値が存在することがわかります。しかも、0を除外すると、取りうる値と取りえない値の個数が等しいこともわかります(例:mod 7なら取りうる値は1と2と4、取りえない値は3と5と6)。
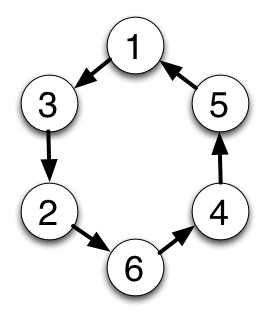
これは偶然ではなく、3以上の全ての素数に成り立つ性質です。たとえばmod 7の世界を考えると、乗算は次の図のようなスゴロク状の盤面で「決まった数だけ進む」操作としてとらえられます。(この図では7の倍数、つまり0は考えないことにします)
この図では6倍は3マス進むことに相当します。5*6 = 30 = 2 (mod 7)を上の盤面上で見ると、5から3マス進めば2である、となります。
ところで、この盤面上で平方数について考えてみましょう。n倍でmマス進むものとすれば、平方数は1*n*nですから、1から数えて2mマス目が平方数です。この盤面ではmは0から5までになるので、平方数は0、2、4マス目である1、2、4しかありえません(mが3以上の場合は1周以上回ることになります)。
mod 7に限らず、奇素数pについて考えると、盤面のマス目の総数はp-1と必ず偶数になり、一方で平方数は全ての偶数マス目になりうるので、平方数が取りうる値と取りえない値は必ず半々になるというわけです。
このあたりの話を真面目に数式で表現するのが数論とか整数論とか呼ばれる分野です。数学の中では比較的とっつきやすい部類だと思うので、連休で暇だなーという方がもしいたら、数学で頭を使ってみてはいかがでしょうか。
まとめ
- 平方数でない数の判定にmod pが利用できます
- どんなpを選ぶかは状況次第だと思います
- ちなみに、mod 4でも50%が平方数でないと判定できます
- 数論は面白いですよ